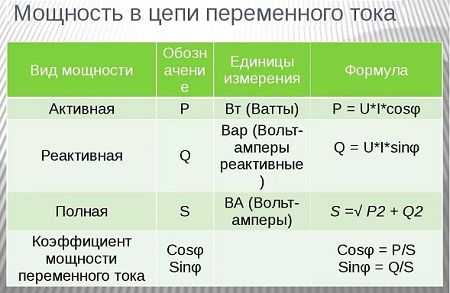
Зависимость мощности от напряжения – , , : » :
Зависимость мощности от силы тока, формула мощности, физический смысл
Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами. Отцом же науки об электричестве считается французский ученый Кулон – именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор. Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно – расстоянию между ними, возведенному в квадрат.
Выясним, что же представляет собой понятие электричество?
Если коротко, то это – направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз
И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются.
А теперь, перейдем к главному.
Основа-основ науки об электричестве – закон Ома.
Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению: сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R
Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах. Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах. Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах. Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом.
Вся остальная электротехника «пляшет» от этого.
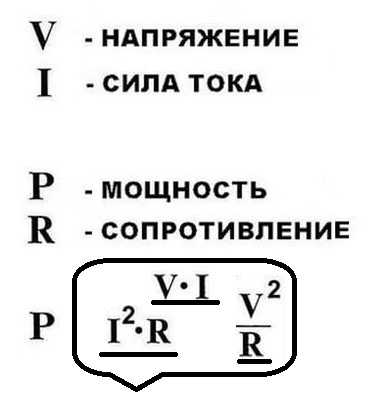
О мощности электрического тока
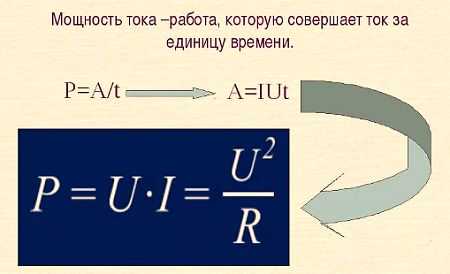
В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.
Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:
P = U*I.
Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление.
Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Вот так – ничего сложного!
pue8.ru
Расчеты напряжения, силы, сопротивления, нагрузки электрического тока
Современная структура общества такова, что на бытовом и промышленном уровне повсеместно используется электроэнергия. Генераторные установки, вырабатывающие электроэнергию, преобразующие подстанции работают для того, чтобы передать ее потребителям на бытовые электрические приборы и промышленные электроустановки.
Общая схема передачи электроэнергии потребителям с учетом мощностей
Что такое мощность электроэнергии
В электросетях, по которым передается энергия, существует ряд основных параметров, которые обязательно учитываются при проектировании и эксплуатации электроустановок.
Одним из таких показателей является электрическая мощность, под этим подразумевается способность электроустановки генерировать, передавать или преобразовывать определенную величину электроэнергии за определенный период времени. Преобразованием считается процесс изменения электрической энергии в тепло, механические движения или другой вид энергии. Чтобы сделать расчет мощности, надо знать, как минимум, величины тока, напряжения и ряда других параметров.
Расчет тока и напряжения, мощности иногда не делают, а измеряют параметры на месте. Но такая возможность не всегда предоставляется. Надо знать, как рассчитать мощность, когда цепь обесточена, при проектировании электроустановок, уметь пользоваться таблицей законов Ома и рассчитать силу тока по известным значениям параметров. Рассчитывать мощность нагрузки и ток нагрузки приходится для того, чтобы правильно выбрать сечение проводов в цепи, величину тока срабатывания для защитных автоматов и других нужд.
Законы Ома наглядно показывают, как посчитать ток по мощности и напряжению
Физический смысл электрической мощности в цепях переменного и постоянного тока одинаковый, но от условий нагрузки в цепи мощность может выражаться разными соотношениями. Для стандартизации закономерности явлений вводится понятие мгновенное значение, что указывает на зависимость скорости преобразований электроэнергии от фактора времени.
Электрическая мощность – это величина, выражающая скорость преобразования энергии электричества в другой вид энергии, обозначается буквой «Р».
Мгновенное значение электрической мощности
Определение – электрическая мощность тесно связана с другими параметрами цепи, током и напряжением, при изменении величины одного из них изменяются другие. Поэтому показания мощности фиксируются в короткий промежуток времени – ∆t.
Напряжение в данном случае обозначают буквой «U» – это выражает разность потенциалов зарядов, перемещенных электрическим полем из одной точки в другую за промежуток времени ∆t.
Сила тока обозначается буквой «I» – это поток, переносимый магнитным полем зарядов, другими словами заряд, перенесенный во временной интервал ∆t.
Исходя из этих определений, просматривается пропорциональная зависимость между этими параметрами:
Р = UxI.
При расчетах можно учитывать зависимость мощности от сопротивления нагрузки «R». По законам Ома для участка цепи с постоянным током мощность выражается как:
Р = I2xR или P = U2|R.
Если поставить в схему питания амперметр и вольтметр, то не придется думать, как вычислить силу тока.
Обратите внимание! Амперметр ставится последовательно в цепь по отношению к сопротивлению нагрузки, а вольтметр – параллельно.
В качестве источника питания используется аккумулятор, как нагрузка установлен прожектор. В данном случае не делается расчет силы тока, параллельно нагрузке подключен вольтметр, для измерения напряжения в Вольтах. Амперметр подключается последовательно для измерения тока в Амперах. Зная показания напряжения и тока по формулам, показанным выше, легко рассчитывается мощность.
Для участков цепи с переменным током формулы расчетов сложнее – необходимо учитывать характер нагрузки.
Расчеты мощности для электроцепей переменного тока
Переменный ток и напряжение имеют синусоидальный вид, при различных нагрузках происходит смещение фазы между ними на определенный угол. По этой причине направление тока иногда может быть противоположным, от нагрузки к источнику питания. Это бывает в электродвигателях, когда обмотка начинает генерировать энергию, это негативно сказывается на эффективности работы оборудования, снижается мощность. При большом количестве потребителей в электросети характер нагрузки имеет смешанный вид, в идеале выделяют три типа нагрузки:
- Активная нагрузка, ее представляют такие электроприборы, как лампы накаливания, нагревательные тэны, спиральные электроплиты;
- Емкостная нагрузка – это конденсаторы в оборудовании различного назначения;
- Индуктивная нагрузка представлена катушками в электродвигателях, обмотках электромагнитов, дросселями и трансформаторами, другими приборами, где ток протекает через обмотки.
Емкостные и индуктивные виды выделяют как реактивную энергию в электросетях. Зная вид нагрузки, расчет потребляемой мощности делается точнее.
Расчет мощности в цепи с активной нагрузкой
Это классический случай в однофазной сети 220 В, в качестве нагрузки можно использовать обычные резисторы. Мощность рассчитывается как произведение действующих значений тока и напряжения, умноженное на соsϕ. В данном случае ϕ – угол смещения между фазами тока и напряжения.
Р = UI cos ϕ
График зависимости мощности по току и напряжению при активной нагрузке
Из графика можно узнать, что колебания тока и напряжения одинаковы по частоте и фазе, мощность всегда положительная с частотой в два раза больше.
Активная электрическая мощность характеризует процесс преобразования в сетях с переменным током энергии в тепло, механические движения, излучение света, в любой вид другой энергии. Измеряется активная нагрузка в Вт, кВт.
Расчет реактивной мощности
Как найти мощность в цепях с индуктивной и емкостной нагрузками? Это делается аналогичным образом. Расчет потребляемой мощности, как и в случае с активной нагрузкой, означает, что действующие напряжение и ток перемножаются, и результат умножается на sin ϕ. Где ϕ – угол сдвига фаз тока и напряжения.
Р = UI sin ϕ
Диаграмма, показывающая взаимосвязь параметров цепи при индуктивной нагрузке
График показывает, что мощность может принимать отрицательные значения, в этот момент энергия отдается в сторону источника питания, фактически она бесполезна и расходуется на нагрев.
Реактивная составляющая энергии характеризует работу нагрузки в виде электронного оборудования, электротехнических схем, моторов с наличием емкостной и индуктивной нагрузки. Единица измерения реактивной мощности при подсчете измеряется в Вар, это (Вольт-Ампер реактивный), обозначается буквой «Q».
Треугольник, отображающий отношение мощностей в сети
Зависимость мощности в цепи переменного тока от реактивной и активной составляющих с учетом угла сдвига фаз хорошо отображается на диаграмме, которую называют треугольником мощностей.
Формула расчета полной мощности обозначается буквой «S»
В этом случае учитывается полный импеданс рассчитываемой мощности электрического тока (комплексное сопротивление нагрузки). Тем, кому вычислением заниматься сложно даже на калькуляторе, можно воспользоваться онлайн калькуляторами на сайте https://www.fxyz.ru с вычислением мощности в цепях с различной нагрузкой. Вычисляется все мгновенно, достаточно заполнить таблицу с исходными параметрами. Когда такой калькулятор под рукой, я вычислю быстро нужные мне параметры.
Видео
Оцените статью:elquanta.ru
Содержание:
Прежде чем рассматривать электрическую мощность, следует определиться, что же представляет собой мощность вообще, как физическое понятие. Обычно, говоря об этой величине, подразумевается определенная внутренняя энергия или сила, которой обладает какой-либо объект. Это может быть мощность устройства, например, двигателя или действия (взрыв). Ее не следует путать с силой, поскольку это различные понятия, хотя и находящиеся в определенной зависимости между собой. Любые физические действия совершаются под влиянием силы. С ее помощью проделывается определенный путь, то есть выполняется работа. В свою очередь, работа А, проделанная в течение определенного времени t, составит значение мощности, выраженное формулой: N = A/t (Вт = Дж/с). Другое понятие мощности связано со скоростью преобразования энергии той или иной системы. Одним из таких преобразований является мощность электрического тока, с помощью которой также выполняется множество различных работ. В первую очередь она связана с электродвигателями и другими устройствами, выполняющими полезные действия. Что такое мощность электрического токаМощность тока связана сразу с несколькими физическими величинами. Напряжение (U) представляет собой работу, затрачиваемую на перемещение 1 кулона. Сила тока (I) соответствует количеству кулонов, проходящих за 1 секунду. Таким образом, ток, умноженный на напряжение (I x U), соответствует полной работе, выполненной за 1 секунду. Полученное значение и будет мощностью электрического тока.
Приведенная формула мощности тока показывает, что мощность находится в одинаковой зависимости от силы тока и напряжения. Отсюда следует, что одно и то же значение этого параметра можно получить за счет большого тока и малого напряжения и, наоборот, при высоком напряжении и малом токе. Это свойство позволяет передавать электроэнергию на дальние расстояния от источника к потребителям. В процессе передачи ток преобразуется с помощью трансформаторов, установленных на повышающих и понижающих подстанциях. Существует два основных вида электрической мощности – активная и реактивная. В первом случае происходит безвозвратное превращение мощности электрического тока в механическую, световую, тепловую и другие виды энергии. Для нее применяется единица измерения – ватт. 1Вт = 1В х 1А. На производстве и в быту используются более крупные значения – киловатты и мегаватты. К реактивной мощности относится такая электрическая нагрузка, которая создается в устройствах за счет индуктивных и емкостных колебаний энергии электромагнитного поля. В переменном токе эта величина представляет собой произведение, выраженное следующей формулой: Q = U х I х sin(угла). Синус угла означает сдвиг фаз между рабочим током и падением напряжения. Q является реактивной мощностью, измеряемой в Вар – вольт-ампер реактивный. Данные расчеты помогают эффективно решить вопрос, как найти мощность электрического тока, а формула, существующая для этого, позволяет быстро выполнить вычисления.
Обе мощности можно наглядно рассмотреть на простом примере. Какое-либо электротехническое устройство оборудовано нагревательными элементами – ТЭНами и электродвигателем. Для изготовления ТЭНов используется материал, обладающий высоким сопротивлением, поэтому при прохождении по нему тока, вся электрическая энергия преобразуется в тепловую. Данный пример очень точно характеризует активную электрическую мощность. Что касается электродвигателя, то внутри него расположена медная обмотка, обладающая индуктивностью, которая, в свою очередь, обладает эффектом самоиндукции. Благодаря этому эффекту, происходит частичный возврат электричества обратно в сеть. Возвращаемая энергия характеризуется небольшим смещением в параметрах напряжения и тока, оказывая негативное влияние на электрическую сеть в виде дополнительных перегрузок. Такие же свойства имеют и конденсаторы из-за своей электрической емкости, когда накопленный заряд отдается обратно. Здесь также смещаются значения тока и напряжения, только в противоположном направлении. Данная энергия индуктивности и емкости, со смещением по фазе относительно значений действующей электросети, как раз и есть реактивная электрическая мощность. Благодаря противоположному эффекту индуктивности и емкости в отношении сдвига фазы, становится возможным выполнить компенсацию реактивной мощности, повышая, тем самым, эффективность и качество электроснабжения. По какой формуле вычисляется мощность электрического токаПравильное и точное решение вопроса чему равна мощность электрического тока, играет решающую роль в деле обеспечения безопасной эксплуатации электропроводки, предупреждения возгораний из-за неправильно выбранного сечения проводов и кабелей. Мощность тока в активной цепи зависит от силы тока и напряжения. Для измерения силы тока существует прибор – амперметр. Однако не всегда возможно воспользоваться этим прибором, особенно когда проект здания еще только составляется, а электрической цепи просто не существует. Для таких случаев предусмотрена специальная методика проведения расчетов. Силу тока можно определить по формуле при наличии значений мощности, напряжения сети и характера нагрузки.
Существует формула мощности тока, применительно к постоянным значениям силы тока и напряжения: P = U x I. При наличии сдвига фаз между силой тока и напряжением, для расчетов используется уже другая формула: P = U x I х cos φ. Кроме того, мощность можно определить заранее путем суммирования мощности всех приборов, которые запланированы к вводу в эксплуатацию и подключению к сети. Эти данные имеются в технических паспортах и руководствах по эксплуатации устройств и оборудования. Таким образом, формула определения мощности электрического тока позволяет вычислить силу тока для однофазной сети: I = P/(U x cos φ), где cos φ представляет собой коэффициент мощности. При наличии трехфазной электрической сети сила тока вычисляется по такой же формуле, только к ней добавляется фазный коэффициент 1,73: I = P/(1,73 х U x cos φ). Коэффициент мощности полностью зависит от характера планируемой нагрузки. Если предполагается использовать лишь лампы освещения или нагревательные приборы, то он будет составлять единицу.
При наличии реактивных составляющих в активных нагрузках, коэффициент мощности уже считается как 0,95. Данный фактор обязательно учитывается в зависимости от того, какой тип электропроводки используется. Если приборы и оборудование обладают достаточно высокой мощностью, то коэффициент составит 0,8. Это касается сварочных аппаратов, электродвигателей и других аналогичных устройств. Для расчетов при наличии однофазного тока значение напряжения принимается 220 вольт. Если присутствует трехфазный ток, расчетное напряжение составит 380 вольт. Однако с целью получения максимально точных результатов, необходимо использовать в расчетах фактическое значение напряжения, измеренное специальными приборами. От чего зависит мощность токаМощность тока, различных приборов и оборудования зависит сразу от двух основных величин – силы тока и напряжения. Чем выше ток, тем больше значение мощности, соответственно, при повышении напряжения, мощность также возрастает. Если напряжение и сила тока увеличиваются одновременно, то мощность электрического тока будет возрастать как произведение той и другой величины: N = I x U.
Очень часто возникает вопрос, в чем измеряется мощность тока? Основной единицей измерения этой величины является 1 ватт (Вт). Таким образом, 1 ватт является мощностью устройства, потребляющего ток силой в 1 ампер, при напряжении 1 вольт. Подобной мощностью обладает, например, лампочка от обычного карманного фонарика. Расчетное значение мощности позволяет точно определить расход электрической энергии. Для этого необходимо взять произведение мощности и времени. Сама формула выглядит так: W = IUt где W является расходом электроэнергии, произведение IU – мощностью, а t – количеством отработанного времени. Например, чем больше продолжается работа электрического двигателя, тем большая работа им совершается. Соответственно возрастает и потребление электроэнергии. |
electric-220.ru
формула, взаимное влияние, нормы, характеристики
 Частота электрического тока выступает одним из параметров качества электроэнергии и основной характеристикой режима энергосистемы. Количественно частота в энергосети равна количеству периодов в секунду. Изменение частоты в сети влияет на функционирование и, соответственно, производительность работы потребителей. Также свое влияние оказывает отклонение частоты на работу всей энергосистемы.
Частота электрического тока выступает одним из параметров качества электроэнергии и основной характеристикой режима энергосистемы. Количественно частота в энергосети равна количеству периодов в секунду. Изменение частоты в сети влияет на функционирование и, соответственно, производительность работы потребителей. Также свое влияние оказывает отклонение частоты на работу всей энергосистемы.
Нормируемые требования к показателям
В РФ требования к качеству работы энергосистемы стандартизированы.
В соответствии с ГОСТ 13109-97 частота в энергосистеме должна непрерывно поддерживаться на уровне f = 50 ± 0,2 Гц, при этом допускается кратковременное отклонение частоты до значения ∆f = 0,4 Гц.
Анализируя зависимость силы тока от частоты, можно сделать вывод, что если подключаемая нагрузка имеет чисто активный характер (к примеру, резистор), то в широком диапазоне сила тока от частоты иметь зависимость не будет. В случае достаточно высоких частот, когда индуктивность и ёмкость подключаемой нагрузки будут характеризоваться сопротивлением, сравнимым с активным, то сила тока будет иметь определенную зависимость от частоты.
Другими словами, при варьировании частоты тока происходит изменение ёмкостного сопротивления, изменение которого, в свою очередь, приводит к изменению тока, протекающего по цепи.
То есть при повышении частоты, снижается ёмкостное сопротивление, и повышается ток, протекающий по цепи.
Математическое выражение зависимости будет иметь следующий вид: I = UCω;
Зависимость при учете активного сопротивления будет определяться следующим выражением: I (ω) = UCω √(R2 • C2 • ω2 + 1).
Влияние частоты тока на электроприборы
Далее рассмотрим влияние частоты электрического тока. Увеличение частоты до сравнительно невысоких величин (1 — 10 тыс. Гц), обычно является следствием исключительно повышения номинальной мощности электроаппаратуры, поскольку таким образом возрастает проводимость газовых промежутков. Для измерения частоты в системе используют частотомеры.
Паровая турбина разрабатываются и создаются таким образом, чтобы при номинальной скорости вращения (частоте) обеспечивалась максимальная выходная мощность на валу. При этом уменьшение номинальной частоты является следствием возникновения потерь на удар пара о лопатки с единовременным повышением момента вращения, а повышение частоты — к снижению момента вращения.
Таким образом, наиболее экономичный режим работы достигается при оптимальной частоте.
Помимо этого, работа на пониженных частотах приводит к ускоренному износу рабочих лопаток и прочих частей и механизмов. Снижение частоты оказывает влияние на расход на собственные нужды станций.
pue8.ru
Зависимость мощности от силы тока и напряжения. Калькулятор зависимости силы тока от напряжения и сопротивления. Ом
Зависимость мощности от силы тока, формула мощности, физический смысл
Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами. Отцом же науки об электричестве считается французский ученый Кулон – именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор. Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно – расстоянию между ними, возведенному в квадрат.
Выясним, что же представляет собой понятие электричество?
Если коротко, то это – направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз
И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются.
А теперь, перейдем к главному.
Основа-основ науки об электричестве – закон Ома.
Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению: сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R
Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах. Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах. Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах. Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом.
Вся остальная электротехника «пляшет» от этого.
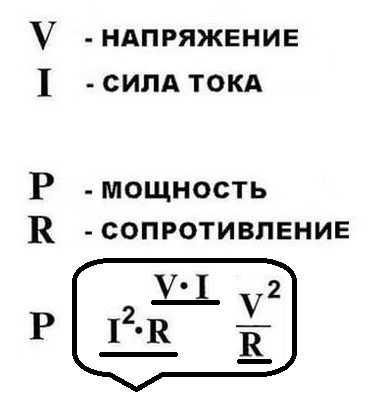
О мощности электрического тока
В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.
Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:
P = U*I.
Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление.
Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Вот так – ничего сложного!
pue8.ru
1.2. Зависимость полезной мощности источника электрического тока от силы тока и внешнего сопротивления
Рассмотрим электрическую цепь, состоящую из источника постоянного тока и внешнего сопротивления R (рис. 1). При протекании тока через такую цепь источником ЭДС выполняется работа и в цепи выделяется мощность.
Полезной мощностью называют мощность, которая выделяется на внешнем сопротивлении. Из закона Джоуля-Ленца (10*) полезная мощность равняется , а из закона Ома для участка цепи. Тогда полезная мощность будет
где – падение напряжения на внешнем сопротивлении. При проте
10i5.ru
Зависимость частоты и напряжений от баланса мощности
Остановимся прежде всего на основном и общем для рассматриваемых задач вопросе: выясним, от чего зависят величины частоты и напряжений, устанавливающиеся в электроэнергетической системе.
Каждый из приемников энергии, присоединенных к электрической сети, потребляет активную и реактивную мощности, величины которых, как уже отмечалось ранее, определяются величиной напряжения на его зажимах и частотой. Мощность, идущая на питание приемников энергии и покрытие потерь в сети, соединяющей приемники с некоторой узловой точкой системы, в данном режиме нагрузки зависит только от частоты и величины напряжения в данной узловой точке.
Следовательно, нагрузка любой узловой точки однозначно (в области нормальных значений частоты и напряжения) определяется частотой и напряжением в этой точке. Статические характеристики нагрузки в некоторой узловой точке представляют собой, как известно, зависимости активной и реактивной мощностей этой нагрузки от напряжения при заданной частоте. Для различных значений частоты может быть построено семейство подобных характеристик (рис. 2).
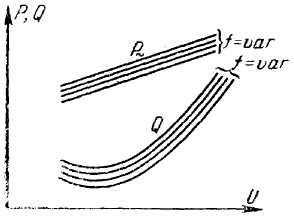
Рис. 2. Зависимости активной и реактивной мощности от напряжения
Обеспечить в данной узловой точке некоторые заданные значения частоты и напряжения можно, только передавая к ней из системы совершенно определенные величины активной и реактивной мощностей. Эти величины при заданных частоте и напряжении можно определить по соответствующим статическим характеристикам нагрузок. Если почему-либо из внешней сети в узловую точку будет поступать недостаточная активная или реактивная мощность, то заданные значения частоты и напряжения не могут установиться в этой узловой точке: параметры фактического режима будут иными. Рассмотрим несколько детальнее этот вопрос.
Пусть заданные семейства статических характеристик выражаются в неявной форме следующими зависимостями:
Величины активной и реактивной мощностей, притекающих к данной узловой точке системы, зависят как от величины U и фазы напряжения в этой узловой точке, так и от величин и фаз напряжений в смежных узловых точках и сопротивлений, соединяющих участки сети.
Допустим сначала для простоты, что напряжения у ближайших узловых точек неизменны по величине и фазе и имеют одинаковую частоту f. Тогда в данной узловой точке установится совершенно определенное напряжение, величина и фаза которого определяются из условия баланса активных и реактивных мощностей: суммарные потоки активной и реактивной мощностей в данную узловую точку (Рг и Qг) должны быть равны соответственно активной и реактивной мощностям нагрузки в данной узловой точке (Рн и Qн). При заданной частоте последние будут только функциями напряжения. Тогда
и
Эти два уравнения с двумя неизвестными и позволяют определить U и .
Покажем, как графически решается эта задача. Совместим на одной диаграмме (рис. 3) характеристику PН = Ф1(U), соответствующую заданному значению f, и семейство характеристик Pг=1(U, ), соответствующих тому же значению f, но при разных значениях . Так как PГ = PН, то из этой диаграммы по точкам пересечения может быть определена зависимость = Ф(U), соответствующая балансу активных мощностей в узловой точке. Далее аналогичным образом совмещаем на одной диаграмме характеристику QH = Ф2(U) и семейство характеристик QГ = 2(U, ) для различных (рис. 4) и заданного f. При помощи найденной зависимости = Ф(U) на каждой из характеристик QГ = 2(U, ) получим точку, находящуюся на характеристике QГ = (U). Соединив эти точки, получим всю характеристику QГ = (U), соответствующую балансу активных мощностей. Тогда точка пересечения характеристик QH = Ф(U) и QГ = (U) определяет фактическое напряжение UН (рис. 4).
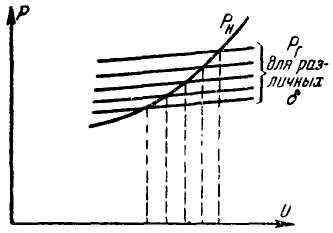
Рис. 3. Определение зависимости угла сдвига (фазы) от величины напряжения
Все наши предыдущие рассуждения относились к случаю неизменности по величине и фазе напряжений в смежных узловых точках и частоты в системе. В действительности такой неизменности нет и напряжения во всех узловых точках могут изменяться по величине и фазе; может также изменяться и частота системы.
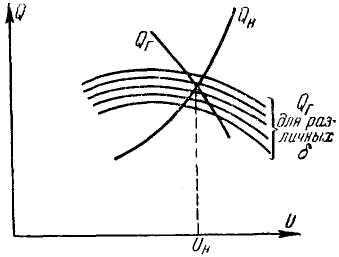
Рис. 4. Построение характеристики зависимости Q от U
Однако в системе можно найти такие узловые точки, в которых поддерживается неизменное по величине и фазе или только по величине напряжение или из которых в сеть передается определенная активная мощность.
При определенном впуске энергоносителя и нормальных значениях параметров режима первичный двигатель развивает мощность, зависящую только от частоты сети, и, следовательно, электромагнитная мощность генератора в этих условиях зависит только от частоты:
Pг=Ф(U).
При постоянстве тока возбуждения генератора неизменной является величина э.д.с. генератора Ed, а при наличии регуляторов возбуждения неизменной или почти неизменной будет величина напряжения на его выводах.
В системе должен быть баланс активных и реактивных мощностей: сумма активных и реактивных мощностей всех генераторов должна равняться сумме активных и реактивных мощностей нагрузок всех узловых точек и потерь активной и реактивной мощностей во всех элементах сетей. Следовательно, частота во всей системе, а также величина и фаза напряжения в каждой из узловых точек установятся как раз такими, которые требуются по условию баланса мощностей.
Пусть в системе установился некоторый режим. Изменим впуск энергоносителя в первичный двигатель одного из генераторов. Угол сдвига ротора этого генератора также изменится. Во всей системе произойдет изменение частоты, а также изменение величин и фаз напряжений во всех узловых точках. Эти изменения будут происходить во времени до тех пор, пока не установится новый режим баланса мощностей в системе. Процесс этот является далеко не таким простым, как можно было бы предполагать. В самом деле, например, уменьшение впуска энергоносителя вызовет уменьшение угла сдвига ротора данного генератора относительно других, активные нагрузки других генераторов возрастут. Появится небаланс на валах каждого из этих генераторов, и они начнут тормозиться. В связи с этим генератор, у первичного двигателя которого уменьшился впуск энергоносителя, также должен начать тормозиться, так как при уменьшении углов сдвига роторов остальных генераторов он должен принять добавочную нагрузку. Торможение всех генераторов будет приводить к снижению общей частоты в системе. По мере ее снижения будут уменьшаться активные мощности нагрузок узловых точек в соответствии с их частотными статическими характеристиками и увеличиваться мощности всех других генераторов в соответствии со статическими характеристиками регуляторов скорости первичных двигателей.
Оба эти фактора приведут к тому, что при достаточно большом снижении частоты вновь наступит баланс на валу каждого из генераторов; мощности, развиваемые первичными двигателями, будут балансироваться с мощностями нагрузки
генераторов. Дальнейшее снижение частоты прекратится. Необходимо учесть, что снижение частоты вызывает изменение Э.Д.С. всех генераторов, реактивных сопротивлений всех ветвей системы, а, следовательно, и всех напряжений в сети, что в свою очередь приведет к изменению активных и реактивных нагрузок всех узловых точек в соответствии с их статическими характеристиками по напряжению и частоте. Таким образом, процесс оказывается достаточно сложным.
Рассмотрим другой случай. Пусть уставка регулятора возбуждения на одном из крупных генераторов системы будет снижена. Тогда уменьшится выпуск реактивной мощности от данного генератора, что приведет к снижению напряжения по крайней мере в близлежащем районе электрической сети. Снижение напряжения в свою очередь вызовет уменьшение активных и реактивных нагрузок всех узловых точек в соответствии с их статическими характеристиками по напряжению. Появится небаланс на валу каждого из генераторов; углы сдвига их роторов, а, следовательно, и скорости их вращения будут расти. Это приведет к повышению частоты, так как генераторы, особенно близлежащие, разгрузятся. Частота в системе будет расти, пока не наступит новый баланс, обусловленный ростом активных нагрузок системы. Рост частоты в свою очередь повлияет на увеличение напряжений.
Такова сложная взаимосвязь изменений частоты, напряжения и активных и реактивных мощностей в системе. Однако для решения практических вопросов можно упростить задачу путем некоторой идеализации.
Так, отвлекаясь от изменений напряжений и реактивных мощностей, можно считать, что изменение баланса активных мощностей в системе определенным образом сказывается только на изменении частоты.
Действительно, рост активной нагрузки потребителей или снижение активной мощности генераторов в первую очередь вызывает определенное для данного режима снижение частоты в системе. Практически именно это является наиболее существенным. Менее существенным является то, что это изменение частоты будет в некоторой степени различным в зависимости от того, в какой узловой точке выросла активная нагрузка или у какого именно генератора снизилась активная мощность. Это различие обусловлено влиянием других факторов (напряжений, реактивных мощностей) и не столь велико. Снижение частоты, обусловленное возникновением дефицита активной мощности, обязательно приведет к восстановлению баланса, так как при этом в связи со снижением частоты и напряжений активная нагрузка уменьшается. В то же время регуляторы скорости первичных двигателей и частоты увеличивают впуск энергоносителя, и активная мощность генераторов растет.
Количественное соотношение, т.е. зависимость относительного изменения частоты от относительного небаланса активной мощности, не является неизменным и в зависимости от режима работы системы может колебаться в довольно широких пределах.
studfiles.net
Зависимость мощности от напряжения. Сопротивление нити лампы накаливания
Сопротивление нити лампы накаливания – блог СамЭлектрик.ру
Решил я как-то проверить закон Ома. Применительно к лампе накаливания. Измерил сопротивление лампочки Лисма 230 В 60 Вт, оно оказалось равным 59 Ом. Я было удивился, но потом вспомнил слово, которое всё объясняло – бареттер.
Дело в том, что сопротивление вольфрамовой нити лампы накаливания сильно зависит от температуры (следствие протекания тока). В моем случае, если это бы был не вольфрам, а обычный резистор, его рассеиваемая мощность при напряжении 230 Вольт была бы P = U2/R = 896. Почти 900 Ватт!
Кстати, именно поэтому производители датчиков с транзисторным выходом рекомендуют соблюдать осторожность при подключении датчиков.
Как же измерить рабочее сопротивление нити лампы накаливания? А никак. Его можно только определить косвенным путем, из закона знаменитого Ома. (Строго говоря, все омметры используют тот же закон – прикладывают напряжение и меряют ток). И мультиметром тут не обойдешься.
Используя косвенный метод и лампочку Лисма 24 В с мощностью 40 Вт, я составил вот такую табличку:
Содержание статьи:
Зависимость сопротивления нити лампы накаливания от напряжения
| Напряжение | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| % напряжения | 8.3 | 16.7 | 25.0 | 33.3 | 41.7 | 50.0 | 58.3 | 66.7 |
| Ток | 0.55 | 0.7 | 0.84 | 0.97 | 1.08 | 1.19 | 1.29 | 1.38 |
| Сопротивление | 3.6 | 5.7 | 7.1 | 8.2 | 9.3 | 10.1 | 10.9 | 11.6 |
| Мощность | 1.1 | 2.8 | 5.04 | 7.76 | 10.8 | 14.28 | 18.06 | 22.08 |
| Напряжение | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| % напряжения | 75.0 | 83.3 | 91.7 | 100.0 | 108.3 | 116.7 | 125.0 | 133.3 |
| Ток | 1.47 | 1.55 | 1.63 | 1.7 | 1.77 | 1.84 | 1.92 | 2 |
| Сопротивление | 12.2 | 12.9 | 13.5 |
samelectric.ru
Какая зависимость мощности от напряжения
Прямо-пропорциональная.
чем больше у тебя мощность, тем больше у других напряжение!
квадратная. мощность пропорциональна току и напряжению, но ток тоже пропорционален напряжению. P=U^2 / R
В общем случае нелинейная, но при сопротивлении. не зависящем от напряжения, U^2/R.
Диаграмма закона Ома тебе в помощь! <img src=”//otvet.imgsmail.ru/download/4862381_01eae08957db3bb7aeb772e3b091465d_800.gif” data-lsrc=”//otvet.imgsmail.ru/download/4862381_01eae08957db3bb7aeb772e3b091465d_120x120.gif” data-big=”1″>
touch.otvet.mail.ru
График зависимости мощности, потребляемой лампой от напряжения на её зажимах! Какой вывод из этого можно сделать?
Если б сопротивление лампы было всё время постоянным, то график был бы параболой (P = U²/R). Но с ростом напряжения и с ростом выделяемой на лампе мощности растёт и температура, а с ней – сопротивление лампы. Так что график будет поначалу параболой, а потом будет расти всё медленнее и медленнее.
P=UI То есть чем больше напряжение, тем больше мощность. Вывод: чем больше у тебя дома мощных приборов, тем больше заплатишь за электроэнергию!))
Невзирая на теорию, все-таки лампа накаливания является нелинейным элементом за счет изменения сопротивления при нагреве и некоторой индуктивной составляющей. Нелинейность незначительна, обычно ей пренебрегают. При превышении номинального напряжения она выходит из строя.
P = U^2 / R. Таким образом, если предположить постоянство сопротивления, мощность пропорциональна квадрату напряжения. На самом же деле, растёт температура, а с ростом температуры и сопротивление, и поэтому завсимость довольно нетривиальная.. . При малых напряжениях зависимость действительно квадратичная, при возрастании напряжения температура начинает сильно влиять на сопротивление и зависимость приближается к линейной. А с дальнейшим ростом вольфрам просто испаряется и лампочка кирдык…
touch.otvet.mail.ru
10i5.ru